算数と数学の違いは？難しいのはどっち？

皆さん、こんにちは。

学び舎エルムの岩間です。

 

 

少しずつ涼しくなり、過ごしやすい季節になってきましたね。

快適な睡眠のおかげで、パッと起きれない日々が続いておりますが、皆さんはいかがお過ごしでしょうか。

 

 

 

さて、今回は小学校で習う「算数」と中学校から始まる「数学」についてご紹介させていただきます。

 

 

「算数」「数学」と聞いて、その違いについて、わかりますか？

小学校では「算数」を習う、中学校に入ると「数学」に変わると、漠然と思っている方も多いのではないでしょうか。

 

 

実は、「算数」と「数学」には考え方に違いがあるのです。

 

 

 

 

早速ですが、ひとつの問題を例に考えてみたいと思います。

 

 

＜問題＞

1枚63円の切手と1枚84円の切手を合わせて30枚買ったら、代金は2268円でした。63円切手と84円切手はそれぞれ何枚買いましたか？

 

 

この問題、中学校で習得する「方程式」を使えば、それほど難しい問題ではありません。

では、xやyのような文字や方程式といった「数学」の知識を使わずに、「算数」の知識で解くことはできますでしょうか？

 

 

 

これが意外と難しいのです。

 

 

算数の知識で解くためには、下の図を用いて考えていきます。

 

 

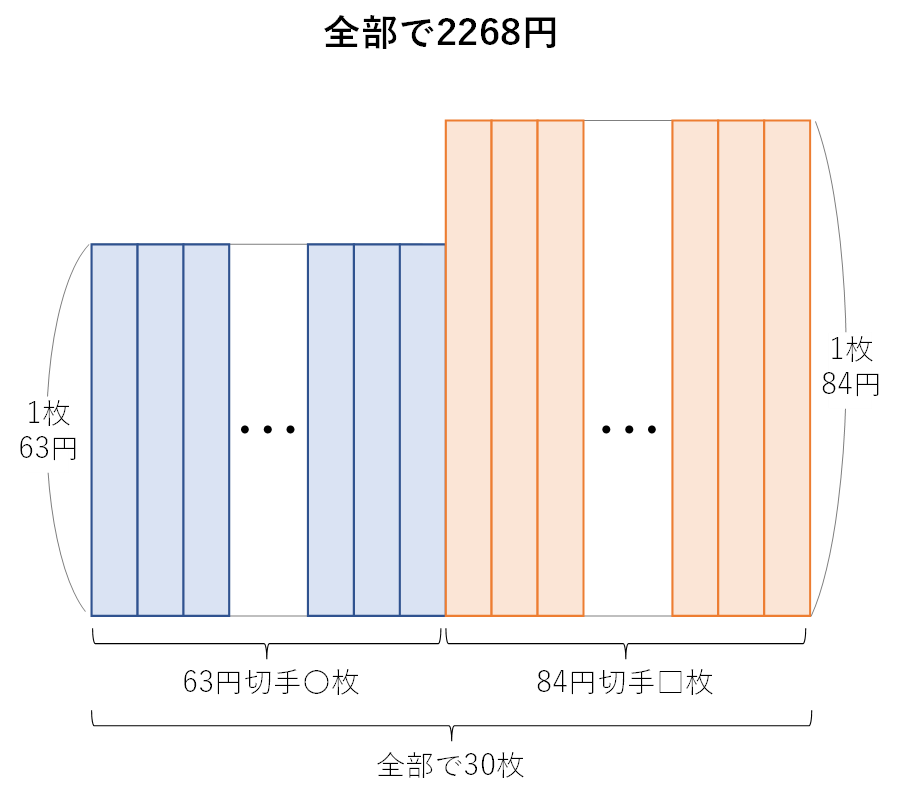
63円切手が〇枚、84円切手が□枚、全部で30枚です。

 

ここで次の図のように、30枚すべてが63円切手だった場合を考えます。

 

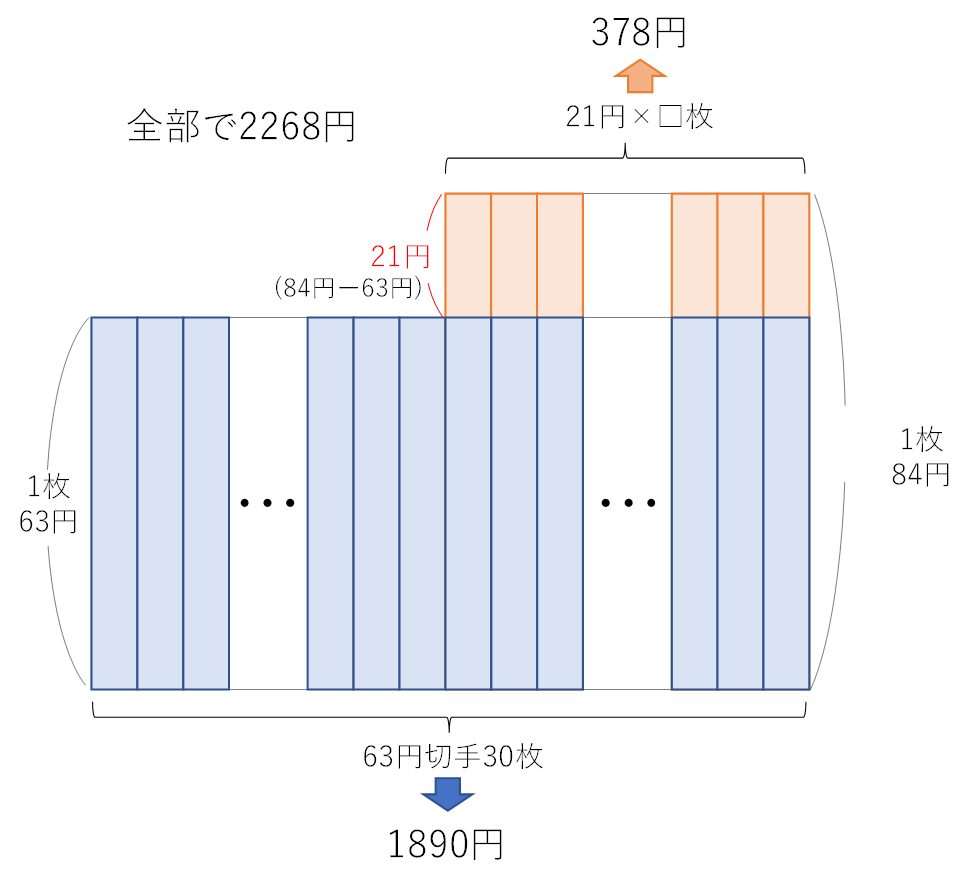
30枚すべてが63円切手だった場合、その金額は63×30＝1890円となります。

合計金額は2268円なので、その差額は2268-1890＝378円です。

 

 

この差額が84円切手と63円切手の差額21円の□枚分となるのです。

□枚は378枚÷21＝18枚となります。

 

このように、63円切手は12枚、84円切手は18枚と解いていきます。

 

 

 

算数の知識では、図を書いて実際の数字をイメージしながら、ロジカルに考えていくのです。

 

 

 

一方で、数学の知識＝方程式を使うと、

購入した84円切手をx枚、63円切手をy枚とおくと次のような式が導かれます。

 

$$84x+63y=2268$$

$$x+y=30$$

 

これを解くと、$$x=18，　y=12$$と同じ答えが導き出されます。

 

 

皆さん、どちらの方が難しかったでしょうか？

方程式を使った方が簡単という方も多いのではと思います。

 

 

「算数」は10個や500円、18kgといった実生活で使われる具体的な量の数字が中心であるのに対して、「数学」はxやyといった文字やマイナス、√（ルート）などの実生活とは少し離れた抽象的思考が必要になってきます。

 

中学校に入り「数学」に苦手意識をもつ子は、この抽象度が上がったことにより、イメージしづらいということが要因としてあげられます。

方程式では式を作って計算すれば、パッと答えが出せるという利便性の反面、式の表す意味や本質を理解せずに進んでしまうというマイナス面もあります。

 

 

そんなときは、具体的な数字でイメージする「算数」に立ち返ってみることも大切かもしれませんね。

 

 

↓ちなみに、休憩時間に算数の問題（差集め算）に挑戦する小中学生たち。

 

 

中学生は方程式を使わずに解くのに夢中になりながら取り組んでおり、解き終わると「ほかに問題はありませんか？」と微笑ましい場面でした。