散布図とは?身近な例から解説します!
2021.09.27ブログ
皆さん、こんにちは。
学び舎エルムの岩間です。
コロナウイルスの新規感染者数が少しずつ減少してまいりましたね。
まだまだ油断のならない状況ですが、学校生活も日常に戻りつつあるようでうれしく思っております。
新規感染者数の推移は、毎日、気になるところです。
日々の報道を見て、東京都は減っているからよい傾向かな…、茨城県は減り方が少ないかな…、などいろいろと思うところはありますね。
都道府県の新規感染者数を見比べてみると、実はそれぞれの値に密接な関係があると気が付きました。
これは、都道府県の新規感染者数データを「散布図(さんぷず)」で比較して読み解いた結果なのです。
ということで、本日は「散布図(さんぷず)」に関する話題をご紹介したいと思います。
散布図は、縦軸と横軸に2つの項目の量や大きさを対応させ、データを点で表したもので、高校1年生で習う内容です。
大学入試共通テストでも散布図の読み取り問題が出題されております。
こちらは大学入試センターのホームページから引用したもので、都道府県の各産業の就業者数割合の読み取りを行う問題です。
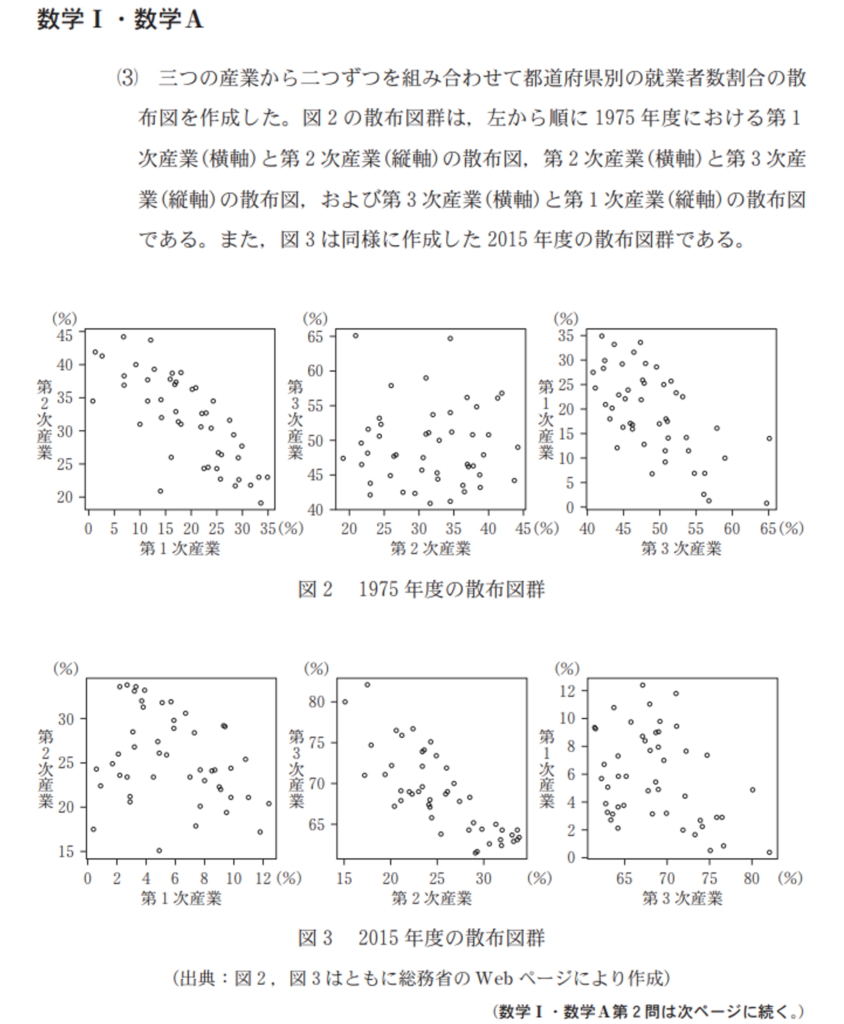
なんだかよくわかりませんね・・・。(汗)
ということで、ここから散布図について、簡単な例をお見せしながらご紹介していけたらと思います。
今回使うデータは以下のものです。
とある屋台のフランクフルトの売上高(円)とアイスの売上高(円)、その日の最高気温(℃)を表しております。
今回のデータはフィクションで、分かりやすくご説明するために、こちらで調整した値になっております。
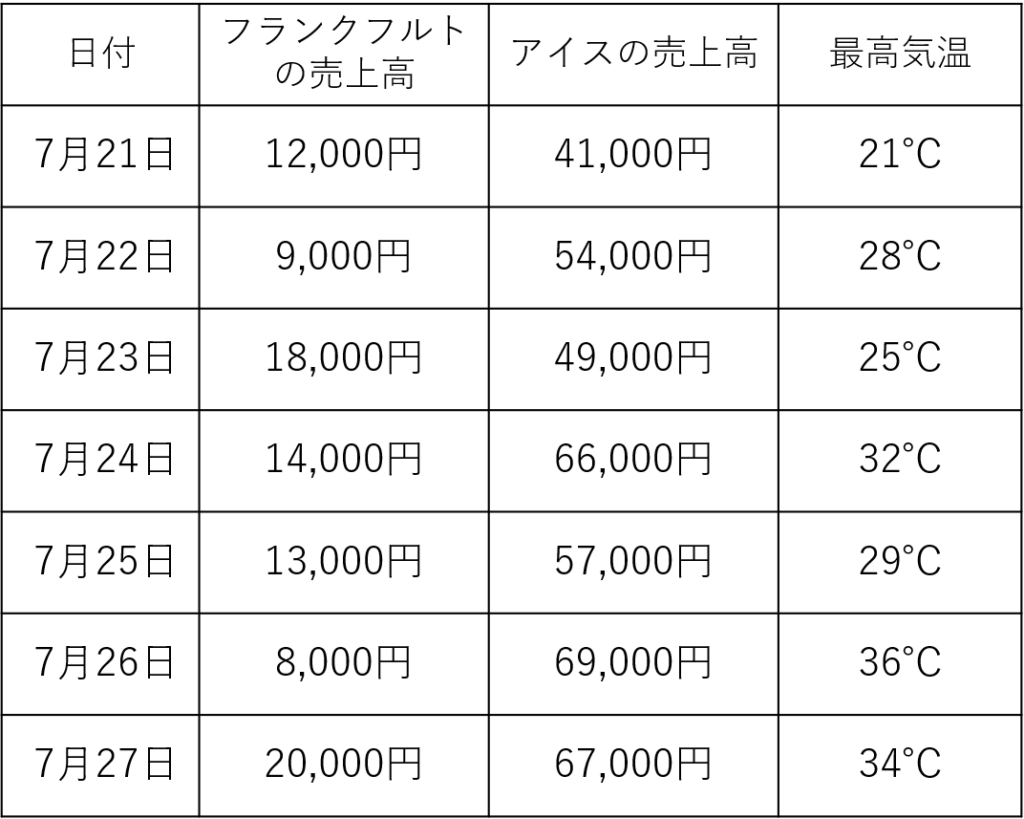
このデータを使用して、散布図を作っていきたいと思います。
まずは最高気温とフランクフルトの売上高の関係をみていきます。
横軸(x軸)を最高気温、縦軸(y軸)をフランクフルトの売上高として、(x, y)を(21℃, 12,000円)、(28℃, 9,000円)・・・(34℃, 20,000円)と値をプロットしていくと次のような散布図になります。
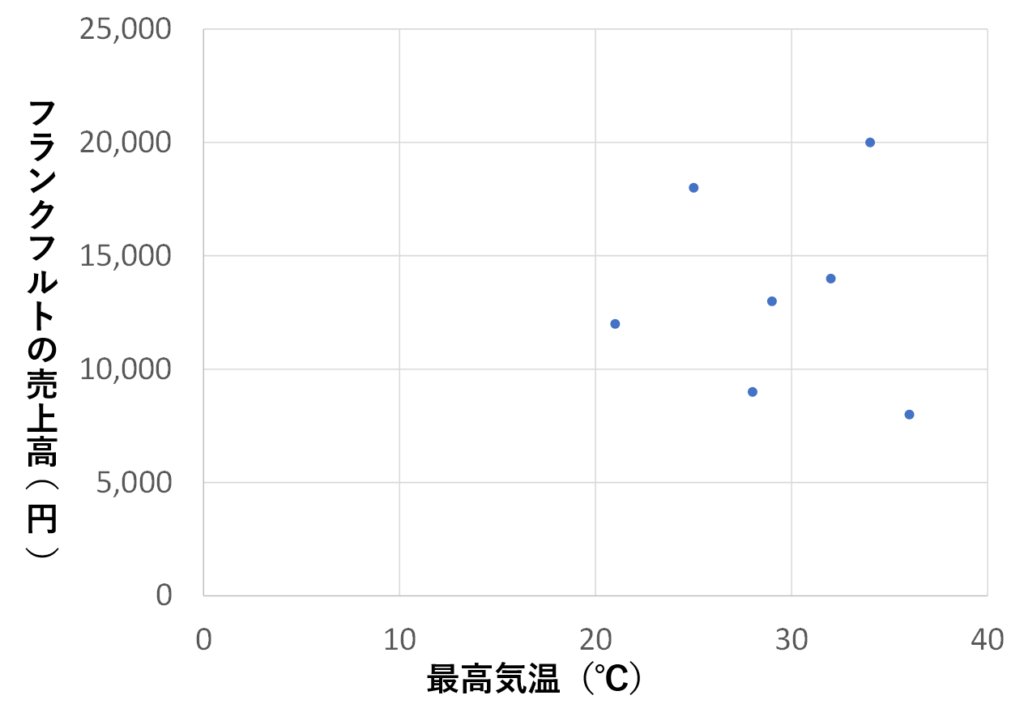
・・・・・・・・・・。
何が読み取れるのか全くわかりませんね。
そうなのです。
ということは、最高気温とフランクフルトの売上高のデータには関係性がないということがわかったのです。
つまり、気温が高くても低くてもフランクフルトは売れるときは売れるし、売れないときは売れないということです。
次に、横軸(x軸)を最高気温、縦軸(y軸)をアイスの売上高として、(x, y)を(21℃, 41,000円)、(28℃, 54,000円)・・・(34℃, 67,000円)と値をプロットしていくと次のような散布図になります。
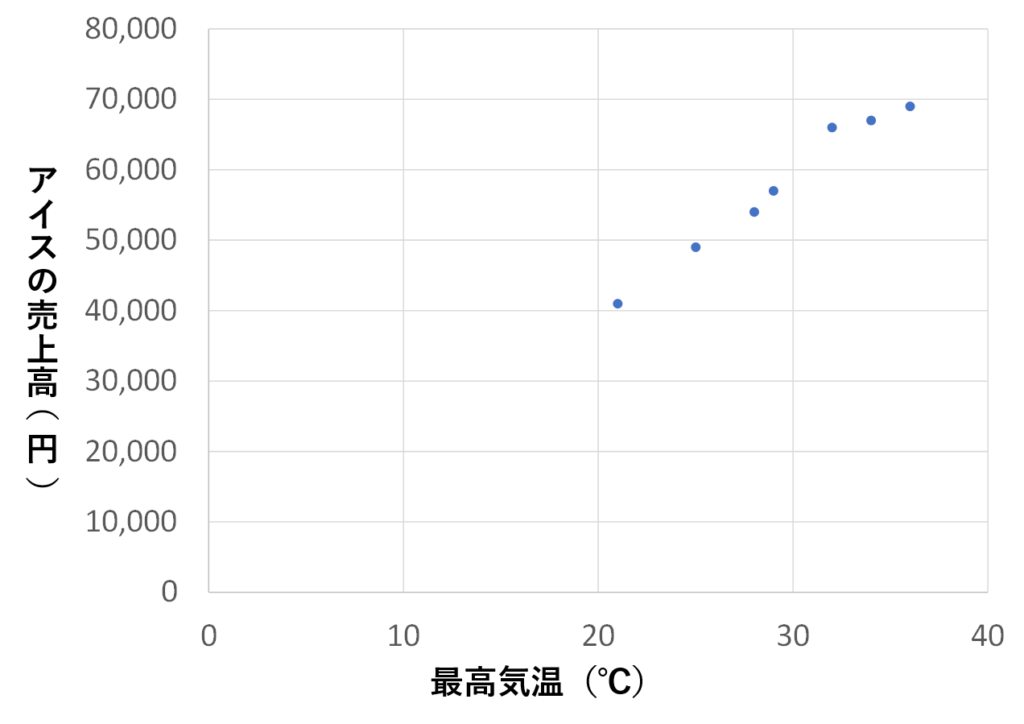
データがきれいに1列に並んでいると思いませんか?
この散布図からは、最高気温が高くなるとアイスの売上高も上がり、最高気温が低くなるとアイスの売上高も下がるということが読み取れます。
これら2つのデータは密接に関わっており、「相関がある」という表現が使われます。
「暑ければアイスはたくさん売れる」ということがデータから読み取れるのです。
このプロットしたデータをうまく通るように赤い線を引いてみました。
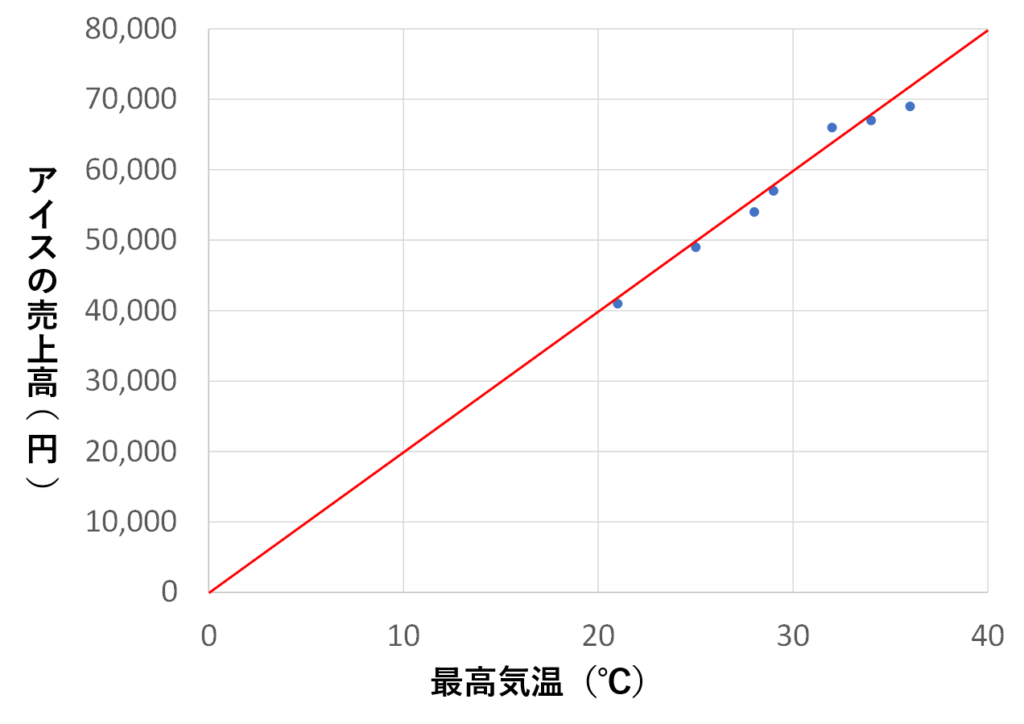
座標上の直線であれば、一次関数$$y=ax+b$$で表すことができます。
中学2年生は前期期末テストに向けて一次関数を勉強中ですから、この赤い直線の式を求められますよね?
この直線の式は
$$y=2000x$$
となります。
だから何?と思うかもしれませんね。
この散布図と一次関数のすごいところは、「売上高の予測を立てられる」ことです。
例えば、明日の最高気温が35℃予想だったとしましょう。
すると、y=2000xの式のxに35を代入すると売上高は70,000円と予測することができるのです!
そして、こういった情報が材料の仕入れや従業員のシフトの調整などに活用できたら、有用だと思いませんか?
散布図はすばらしい!
そして、一次関数はめちゃめちゃ便利です!
ただ、今回は都合よくデータをいじっているから、きれいに並んで当然では・・・。
そうですね。かなり調整しました。笑
(散布図を簡単に説明するという意味で間違ったことはしておりませんのでご安心ください)
では、実際のデータから得られる散布図はどのように表されるのでしょうか?
ということで、最後に実際のデータ「都道府県のコロナウイルス新規感染者数」から散布図を作ってみたいと思います。
このデータはNHKのホームページからダウンロードしたもので、実際のデータです。
(ノンフィクションです!)
2021年1月1日~9月24日の期間のデータで散布図を見ていきましょう。
まずは横軸に茨城県の新規感染者数、縦軸に同じ日の東京都の新規感染者数をあてはめた散布図です。
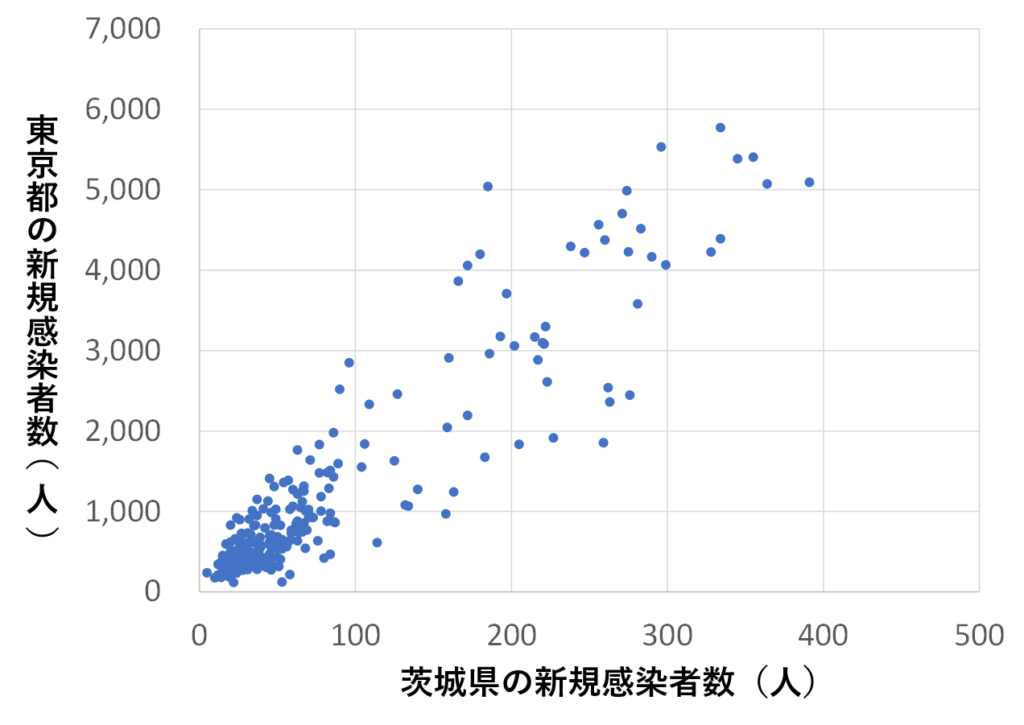
きれいな1本の直線にはなっておりませんが、右上がりの傾向で、相関があります。
東京都の新規感染者数が多い時は、茨城県の新規感染者数も多く、東京都が少ない時は茨城県も少ないということが読み取れます。
ここで茨城県と青森県の新規感染者数の散布図を作ると次のようになりました。
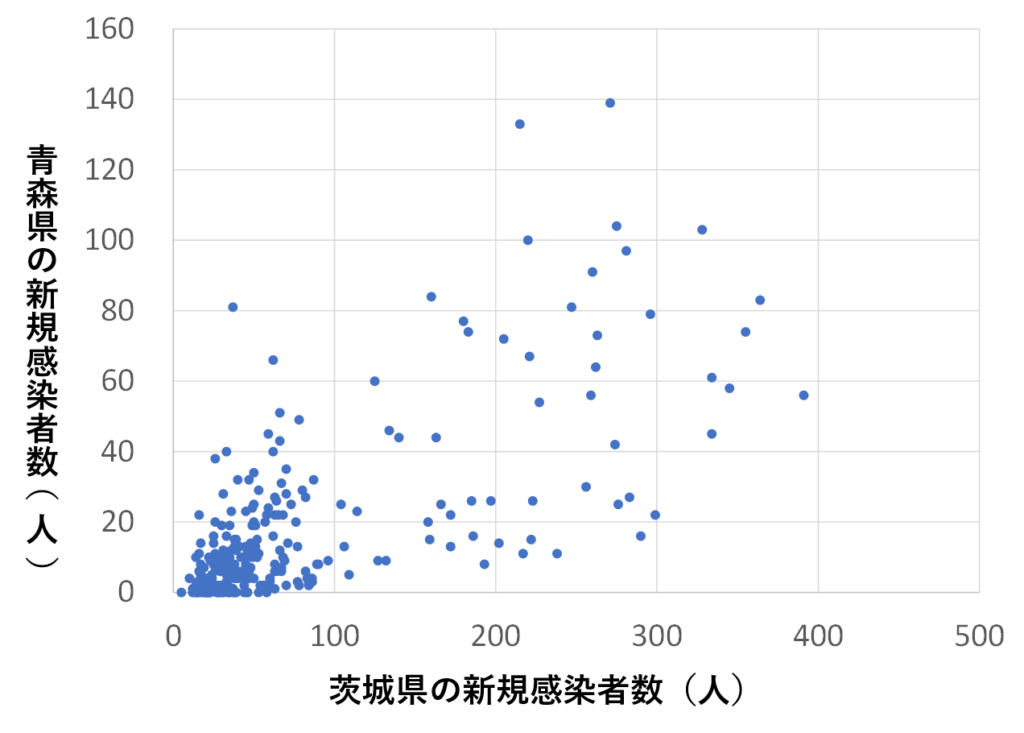
うっすら右上がり・・・?な傾向は見えなくもないですが、相関はなさそうです。
ということは、人の往来が多い東京都と茨城県では、感染状況に密接な関係があるということです。
データ上では、茨城県の新規感染者数を減らすには、東京都の新規感染者数を減らさなければならない訳ですから、都道府県の横断的な対策も有効になってくるわけですね。
最後に、神奈川県と、神奈川県からは遠く離れた北海道の新規感染者数の散布図を見て終わりたいと思います。
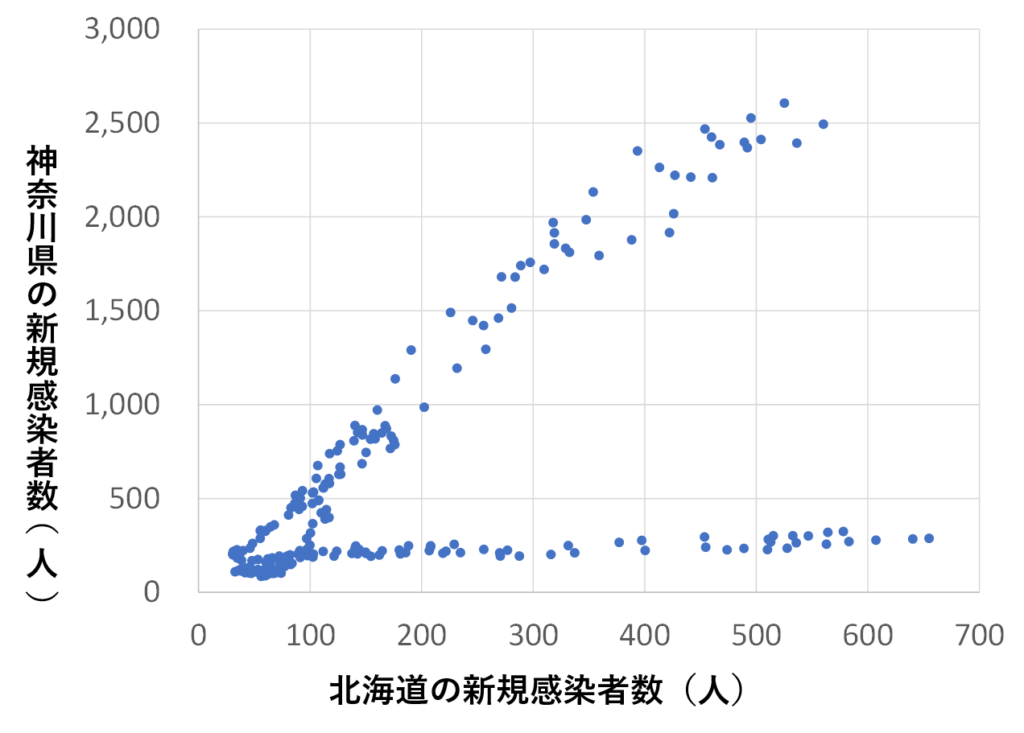
神奈川県と北海道は遠く離れておりますが、かなり強い相関がありますね。
そして、明確な2本のラインが見えます。
横ばいになっているラインはどういう状況なのか?というと、北海道の新規感染者数は増えても神奈川県の新規感染者数はそれほど増えていないということです。
このラインの期間はざっくり今年の4月下旬から6月上旬までで、北海道では爆発的な感染拡大をしていたことが読み取れるのです。
いろいろとご紹介させていただきましたが、このようにデータからは様々な情報を読み取ることができます。
今回とは期間や条件を変更するとまた別の傾向が見えたりと、データって非常に興味深いです。
今回ご紹介した内容は、いわゆるお勉強からは大分外れておりますが、いつか子どもたちにも興味を持ってもらえる、きっかけを提供できたらと思い描いております。
最後までお読みいただきありがとうございました!





